Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
In this blog post, we will go over the NeurIPS 2022 paper titled Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. This paper introduces Chain of Thought (CoT) prompting, which augments few-shot training samples for in-context learning with explicit reasoning steps. The authors evaluate the effectiveness of CoT on math word problems, commonsense reasoning and symbolic reasoning and shows performance improvements from the standard prompting as well as fine-tuned GPT-3 with smaller number of parameters.
Outline of this blog post:
- Introduction
1.1. Motivation behind chain-of-thought prompting
1.2. What is Chain of Thought Prompting anyway?
1.3. Attractive Properties of CoT Prompting - Experiments
2.1. Arithmetic Reasoning
2.1.1. Benchmarks & Results
2.1.2. Ablation Study
2.1.3. Robustness of Chain of Thought
2.2. Commonsense Reasoning
2.2.1. Benchmarks & Results
2.3. Symbolic Reasoning
2.3.1. Tasks & Results - Conclusions
- References
1. Introduction
1.1 Motivation behind chain-of-thought prompting
Language models have transformed the field of natural language processing by improving performance and sample efficiency. However, increasing the size of models alone does not guarantee high performance on challenging tasks such as arithmetic, commonsense, and symbolic reasoning. This paper proposes a method called “chain-of-thought prompting” which is inspired by several prior directions: prompting, natural language explanations, program synthesis/execution, numeric and logical reasoning, and intermediate language steps. The recent success of large-scale language models has led to growing interest in improving their capability to perform tasks via prompting (Brown et al., 2020).
CoT prompting combines two ideas to unlock the reasoning ability of large language models:
Firstly, generating natural language rationales can improve arithmetic reasoning.
Prior work has generated natural language intermediate steps by training from scratch or finetuning a pretrained model, as well as neuro-symbolic methods that use formal languages instead of natural language (Roy and Roth, 2015; Chiang and Chen, 2019; Amini et al., 2019; Chen et al., 2019).
Secondly, large language models can perform in-context few-shot learning via prompting, which means that instead of finetuning a separate language model for each new task, one can simply “prompt” the model with a few input–output exemplars demonstrating the task.
Empirical evaluations on arithmetic, commonsense, and symbolic reasoning benchmarks demonstrate that CoT prompting outperforms standard prompting. This approach is important because it does not require a large training dataset and a single model checkpoint can perform many tasks without loss of generality.
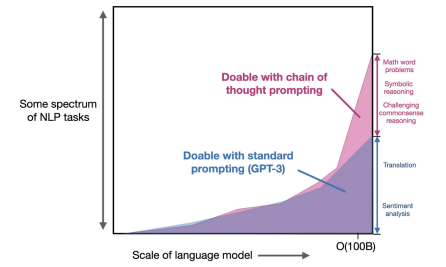
1.2. What is Chain-of-Thought Prompting anyway?
A chain of thought is a series of intermediate natural language reasoning steps that lead to the final output, and this approach is called chain-of-thought prompting. An example prompt is shown in the figure below.
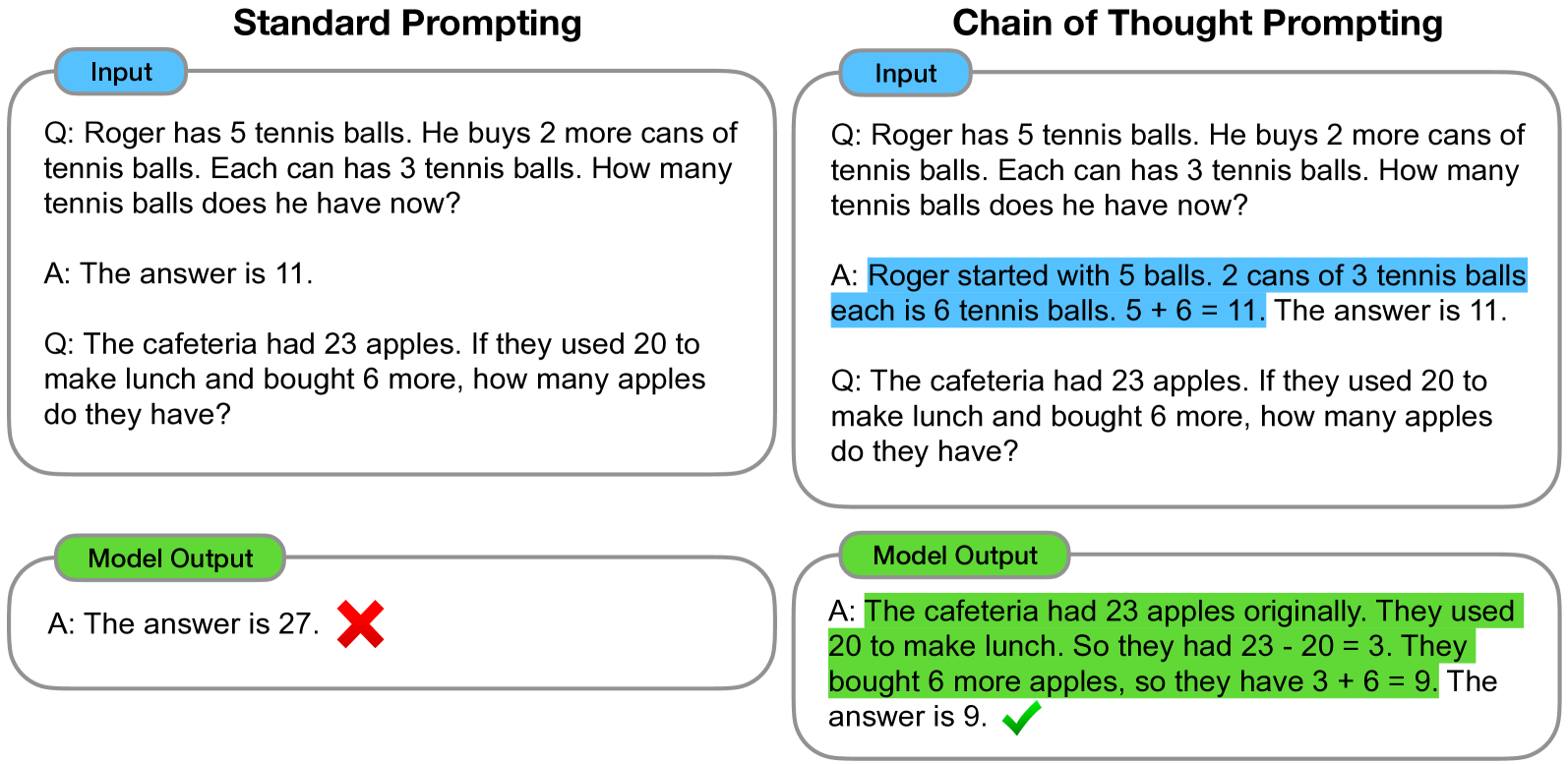
The first method, called “standard prompting” (popularized by GPT-3), involves providing the model with input-output pairs (questions and answers) before asking it to predict the answer for a test example. The second method, called “chain of thought prompting,” involves prompting the model to generate intermediate reasoning steps before giving the final answer to a problem. The goal is to simulate an intuitive thought process that humans might use when working through a multi-step reasoning problem. While previous methods have used fine-tuning to produce such thought processes, the authors show that CoT prompting can elicit these processes by providing a few examples of the CoT without requiring a large training dataset or modifying the language model’s weights.
1.3. Attractive Properties of CoT Prompting
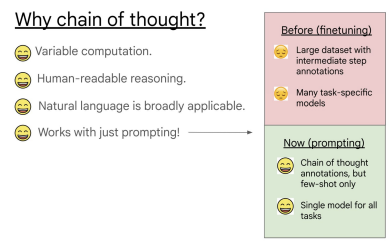
The approach of CoT prompting has several advantages for enabling reasoning in language models:
- It allows models to break down multi-step problems into intermediate steps, which enables them to allocate additional computation for problems that require more reasoning steps.
- A CoT offers an interpretable view of the model's behavior, indicating how it might have reached a specific answer and allowing for debugging if the reasoning process goes wrong.
- Chain-of-thought reasoning can be used for a range of tasks like math word problems, commonsense reasoning, and symbolic manipulation, and can potentially be applied to any task that humans solve via language.
- It can be quickly elicited in large off-the-shelf language models by providing examples of CoT sequences as exemplars for few-shot prompting.
Empirical experiments that will be discussed below show the effectiveness of CoT prompting for arithmetic reasoning (Section 2.1), commonsense reasoning (Section 2.2), and symbolic reasoning (Section 2.3).
2. Experiments
2.1. Arithmetic reasoning
Let’s start with math word problems of the form in the above figure, which measure the arithmetic reasoning ability of language models. Though simple for humans, arithmetic reasoning is a task where language models often struggle to use logical deduction and problem-solving skills. In the context of natural language processing and artificial intelligence, arithmetic reasoning tasks are used to evaluate the ability of language models to perform mathematical calculations and solve mathematical word problems.
2.1.1 Benchmarks & Results
Chain-of-thought prompting is here explored for various language models on multiple benchmarks. Five math word problem benchmarks include: (1) the GSM8K benchmark of math word problems, (2) the SVAMP dataset of math word problems with varying structures, (3) the ASDiv dataset of diverse math word problems, (4) the AQuA dataset of algebraic word problems, and (5) the MAWPS benchmark.

Standard prompting. For the baseline, we consider standard few-shot prompting, in which a language model is given in-context exemplars of input–output pairs before outputting a prediction for a test-time example. Exemplars are formatted as questions and answers. The model gives the answer directly, as shown in the second figure above (left).
CoT Prompting. The proposed method involves adding a CoT for each example in the few-shot prompting dataset. The researchers manually created eight few-shot examples with chains of thought for prompting since most datasets only have an evaluation split (the second figure, right). To test the effectiveness of CoT prompting for various math word problems, the same set of eight CoT exemplars was used for all benchmarks except AQuA, which is multiple-choice and uses four exemplars and solutions from the training set. The table below shows few-shot exemplars for CoT prompting for some datasets.

The task is performed by five large language models. The first is GPT-3, for which text-ada-001, text-babbage-001, text-curie-001, and text-davinci-002 models are used, which presumably correspond to InstructGPT models of 350M, 1.3B, 6.7B, and 175B parameters. The second is LaMDA, which has models of 422M, 2B, 8B, 68B, and 137B parameters. The third is PaLM, which has models of 8B, 62B, and 540B parameters. The fourth is UL2 20B, and the fifth is Codex. They sample from the models via greedy decoding (though follow-up work shows chain-of-thought prompting can be improved by taking the majority final answer over many sampled generations).
Results. The strongest results of chain-of-thought prompting are summarized in the figure below. There are three key takeaways:
- CoT prompting does not improve performance for small models and is only effective for models of ~ 100 B parameters. Smaller models produced fluent but illogical chains of thought, resulting in lower performance than standard prompting.
- CoT prompting has larger performance gains for more complicated problems. It doubled performance for the largest GPT and PaLM models on the GSM8K dataset, which had the lowest baseline performance. However, it had negative or very small improvements for the SingleOp subset of MAWPS, which only requires a single step to solve.
- CoT prompting using GPT-3 175B and PaLM 540B compares favorably to prior state of the art, which usually involves fine-tuning a task-specific model on a labeled training dataset. PaLM 540B achieves new state of the art on GSM8K, SVAMP, and MAWPS using chain-of-thought prompting.
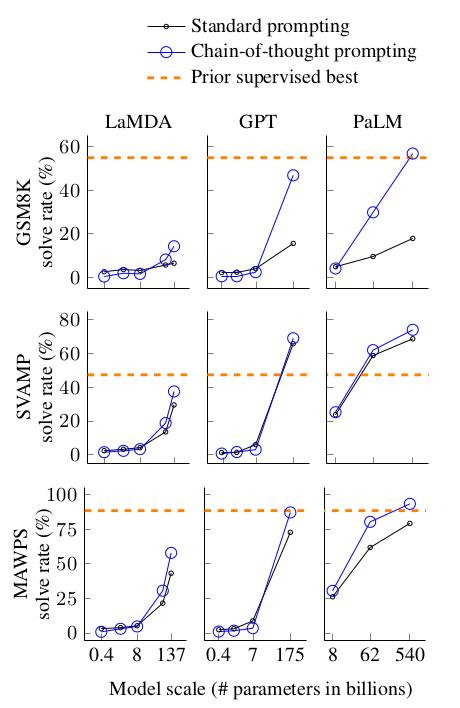
To understand why CoT prompting works, a manual examination of LaMDA 137B model-generated CoT for GSM8K was done. The analysis found that 50 randomly selected examples where the model returned the correct final answer, all of the generated CoTs were logically and mathematically correct except for two coincidences. The analysis also examined 50 random samples where the model gave the wrong answer, finding that 46% of the CoTs were almost correct, with minor mistakes, and that 54% had major errors in semantic understanding or coherence. A similar analysis of errors made by PaLM 62B was performed and it showed that scaling to PaLM 540B improved its one-step missing and semantic understanding errors.
2.1.2. Ablation Study
Given the observed benefits of using CoT prompting, can we say that the same performance improvements can be conferred via other types of prompting? To answer this question, let’s look at the ablation study shown in the figure below with three variations of CoT.
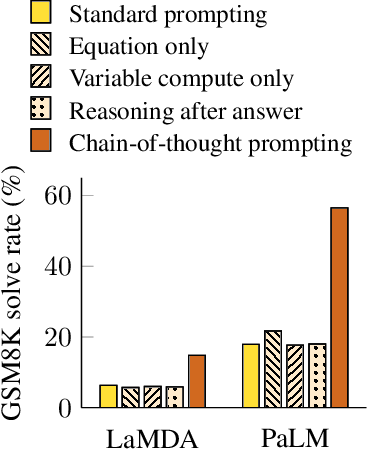
Equation only. The first variation prompts the model to output only a mathematical equation before giving the answer, but the figure below shows that this does not help much for the GSM8K dataset, implying that the semantics of the questions in GSM8K are too challenging to directly translate into an equation without the natural language reasoning steps.
Variable compute only. The second variation isolates the effect of variable computation from CoT reasoning by prompting the model to output only a sequence of dots equal to the number of characters in the equation needed to solve the problem, but this performs about the same as the baseline, suggesting that variable computation by itself is not the reason for the success of CoT prompting.
Chain of thought after answer. The third variation tests whether the model actually depends on the produced CoT to give the final answer by giving the CoT prompt only after the answer, but this performs about the same as the baseline, suggesting that the sequential reasoning embodied in the CoT is useful for reasons beyond just activating knowledge.
2.1.3. Robustness of Chain of Thought
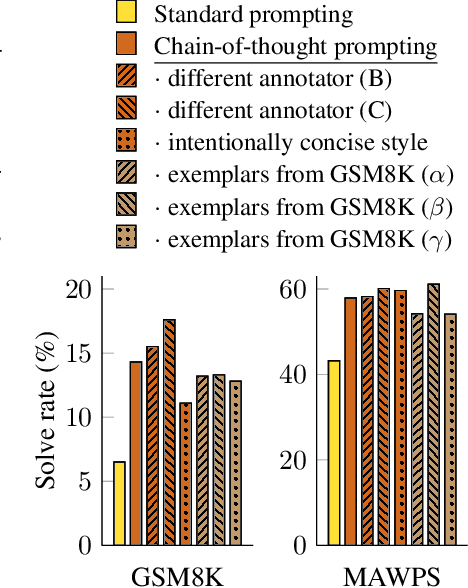
The robustness of CoT prompting is evaluated by different chains of thought written by different annotators. Three co-authors of the paper independently wrote CoTs for the same few-shot exemplars, and a comparison of the results for LaMDA 137B on GSM8K and MAWPS in the figure below shows that all sets of CoT prompts outperform the standard baseline by a large margin, implying that successful use of CoT does not depend on a particular linguistic style. Additionally, experiments with three sets of eight exemplars randomly sampled from the GSM8K training set show that these prompts performed comparably with the manually written exemplars, also substantially outperforming standard prompting. Finally, the study finds that CoT prompting for arithmetic reasoning is robust to different exemplar orders and varying numbers of exemplars.
2.2. Commonsense reasoning
In addition to arithmetic reasoning, we consider whether the language-based nature of CoT prompting also makes it applicable to commonsense reasoning, which involves reasoning about physical and human interactions under the presumption of general background knowledge.
2.2.1. Benchmarks & Results
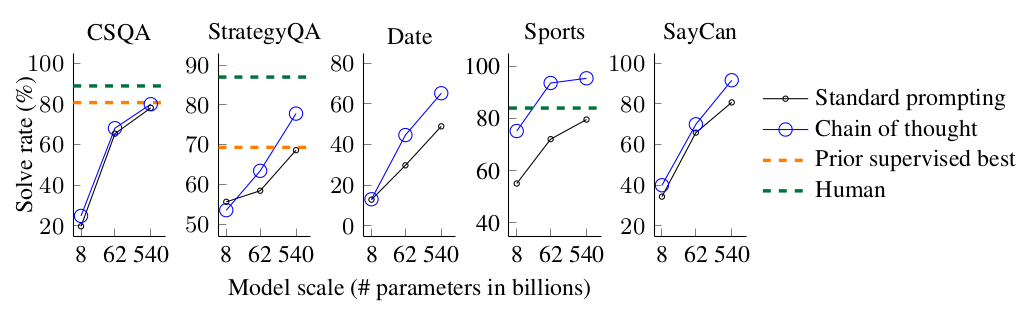
For these evaluations, we observe the CommonsenseQA and StrategyQA benchmarks, as well as two domain-specific tasks from BIG-Bench collaboration regarding date understanding and sports understanding. In addition, the SayCan dataset involves mapping a natural language instruction to a sequence of robot actions from a discrete set.

We follow the same experimental setup for prompts as the prior section.
Results. The full results for LaMDA, GPT-3, and different model scales are shown in the table below.
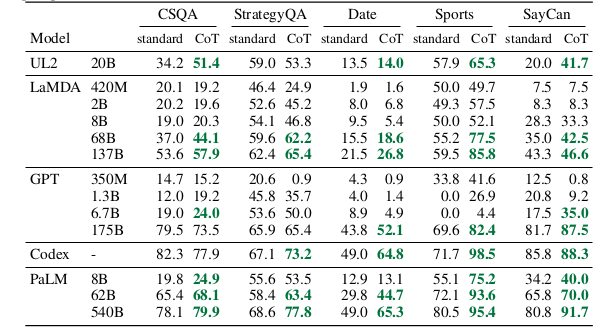
The figure below shows that PaLM of a bigger size performed best in all tasks, indicating the gain of CoT prompting. PaLM 540B achieved higher improvement compared to baselines and exceeded the prior state of the art on StrategyQA (75.6% vs 69.4%) and outperformed sports enthusiasts on sports understanding (95.4% vs 84%).
2.3. Symbolic reasoning
Our final experimental evaluation considers symbolic reasoning, which is simple for humans but potentially challenging for language models.
2.3.1. Tasks & Results
We use the following two toy tasks:
1. Last letter concatenation. This task asks the model to concatenate the last letters of words in a name. It is a more challenging version of first letter concatenation, which language models can already perform without chain of thought.
2. Coin flip. This task asks the model to answer whether a coin is still heads up after people either flip or don’t flip the coin.

The performance of language models on symbolic reasoning tasks is evaluated using in-domain and out-of-domain test sets for which evaluation examples had more steps than those in the few-shot exemplars. For last letter concatenation, the model only sees exemplars of names with two words, and then performs last letter concatenation on names with 3 and 4 words. We do the same for the number of potential flips in the coin flip task. The experimental setup uses the same methods and models as in the prior two sections.
Results. As shown in the table below, with PaLM 540B, CoT prompting leads to almost 100% solve rates. It is worth to note that standard prompting already solves coin flip with PaLM 540, but not for LaMDA 137B.
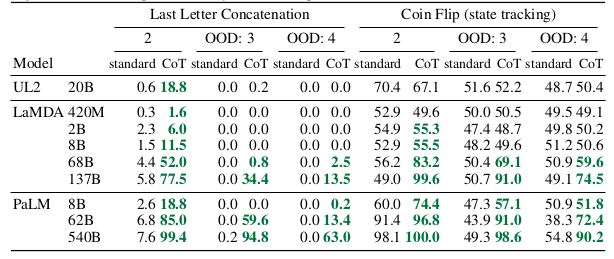
Overall results demonstrate that small models still fail and the ability to perform abstract manipulations on unseen symbols for these three tasks only arises at the scale of 100B model parameters. As for the out-of-domain evaluations, standard prompting fails for both tasks. With CoT prompting, language models achieve better results, although performance is lower than in the in-domain setting. Hence, chain-of-thought prompting facilitates symbolic reasoning beyond seen chains of thought for language models of sufficient scale.
3. Conclusions
In this blog post, we provided a better understanding of chain-of-thought prompting for multi-step reasoning behavior in large language models. The experiments of the paper Chain-of-Thought Prompting Elicits Reasoning in Large Language Models showed that CoT prompting improves performance on arithmetic, commonsense, and symbolic reasoning tasks, and allows large language models to perform tasks that they would otherwise be unable to. Although CoT prompting has its own limitations such as the cost of manual annotation and the lack of guarantee of correct reasoning paths, the paper suggests that this is a simple and broadly applicable method for enhancing reasoning in language models, and may inspire further work on language-based approaches to reasoning.
4. References
Subhro Roy and Dan Roth. 2015. Solving general arithmetic word problems. EMNLP